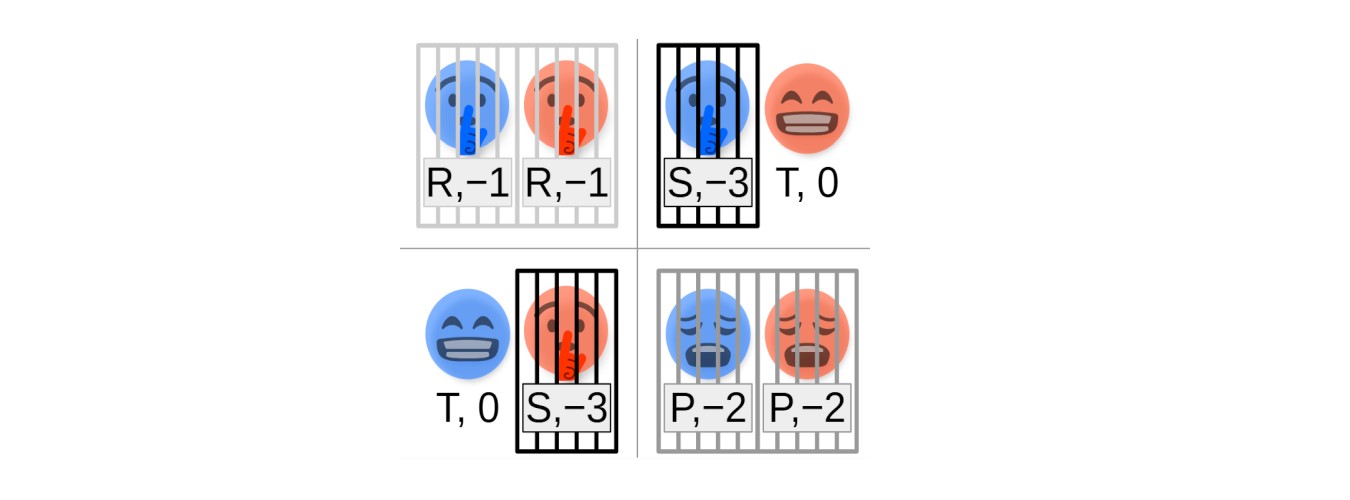
Indywidualny rozsądek każe nam nie współpracować i podpowiada, że najlepiej korzystać z dóbr wytworzonych przez nieracjonalnych altruistów, choć gdyby wszyscy ze sobą kooperowali, byłoby więcej dóbr do podziału. Paradoks ten stanowi istotę tzw. dylematów społecznych.
Matematyczna teoria gier opisuje układy oddziałujących ze sobą osobników (graczy), którzy mogą się zachowywać na różne sposoby zwane strategiami. Gracze w wyniku rozgrywki uzyskują korzyści w postaci wypłat, których wysokość jest uzależniona nie tylko od ich strategii, ale także od strategii ich oponentów. Jest to fundamentalna cecha teorii gier, odróżniająca ją od klasycznej optymalizacji, w której szukamy najlepszego, czyli optymalnego dla siebie rozwiązania w odpowiedzi na niezmienne warunki zewnętrzne. W teorii gier działania każdego gracza wpływają na jego otoczenie, ale otoczenie wpływa też na jego zachowania. Podstawowe założenie indywidualnej racjonalności mówi, że każdy gracz dąży do uzyskania jak największej wypłaty, nie bacząc na innych. Wybierając strategię, musi wziąć pod uwagę zachowania swoich oponentów, a także przewidzieć, czego oni się po nim spodziewają.
Tego typu rozważania doprowadziły Johna Nasha do sformułowania koncepcji równowagi. Jest to taki wybór strategii przez graczy, że żadnemu z nich nie opłaca się zmiana, gdyż na pewno sobie nie podwyższy wypłaty, a być może ją obniży. Powstaje wtedy niepisany kontrakt, którego jednostronne zerwanie nie przynosi korzyści. Równowaga Nasha zapewnia pewien rodzaj bezpieczeństwa, ale czy zapewnia graczom optymalne wypłaty?
Klasycznym przykładem ilustrującym istotę dylematów społecznych jest „Dylemat więźnia”:
Dwie osoby oskarżone o popełnienie przestępstwa są oddzielnie przesłuchiwane. Każda może zeznawać przeciwko wspólnikowi (zdrada – Z) lub milczeć (kooperacja – K). Jeżeli żaden z oskarżonych nie zgodzi się współpracować z policją i obydwaj wybiorą strategię „kooperacja”, uzyskają obniżenie wyroków o 3 lata. Gdy jeden będzie chronił wspólnika („kooperacja”), ale drugi zdecyduje się na ugodę („zdrada”), pierwszy dostanie wyrok maksymalny, a drugi – niższy o 5 lat. Jeśli przestępcy oskarżą się wzajemnie (każdy zagra „zdrada”), mogą liczyć na złagodzenie kary o 1 rok.
Obniżenie wyroku można traktować jako wypłaty w grze „Dylemat więźnia” i zaprezentować je za pomocą następującej macierzy wypłat, gdzie gracz wierszowy, grając strategią wierszową K lub Z przeciwko graczowi kolumnowemu grającemu K lub Z, otrzymuje wypłatę daną na przecięciu odpowiedniego wiersza i kolumny.
| K | Z | |
| K | 3 | 0 |
| Z | 5 | 1 |
Jak widać, niezależnie od strategii jednego gracza drugiemu opłaca się go zdradzić, obopólna zdrada jest równowagą Nasha. Jednak obaj gracze uzyskaliby większe złagodzenie wyroku, gdyby ze sobą współpracowali. Mamy tu do czynienia z przykładem dylematu społecznego w najbardziej elementarnej postaci. Co robić? Jak wydostać się z równowagi Nasha?
Rozszerzeniem klasycznej teorii gier jest teoria gier ewolucyjnych zaproponowana przez Johna Maynarda-Smitha w latach 70. XX wieku. Niedługo potem pojawiły się jej konkretne modele dynamiczne. W najprostszym ujęciu różnica polega na tym, że w grze uczestniczy wielu osobników. Gracze łączą się w pary i rozgrywają np. „Dylemat więźnia”. W kolejnej rundzie proporcja graczy wybierających określoną strategię zmienia się w zależności od wypłaty, jaką zastosowana strategia przyniosła w poprzedniej rundzie. Wynika to bezpośrednio z istoty teorii ewolucji Darwina: osobniki lepiej przystosowane mają więcej dzieci, które dziedziczą ich cechy, a w tym przypadku cechami tymi są strategie gry.
Robert Axelrod rozszerzył zbiór dopuszczalnych strategii i przeprowadził komputerowe rozgrywki zgodnie z powyżej opisanymi zasadami. Rozszerzenie zasad było konieczne, ponieważ gdybyśmy dopuścili tylko bezwarunkową zdradę lub bezwarunkową kooperację, to populację bardzo szybko zdominują zdrajcy. Okazało się, że całkiem nieźle sprawdzała się strategia „wet za wet” (z ang. tit for tat): w pierwszej rundzie współpracujemy, a w następnych postępujemy tak, jak oponent zachowywał się w poprzedniej rundzie, czyli zdradzamy zdrajcę, a kooperujemy z altruistą. Strategia ta wygrywała z wieloma innymi, ale jak łatwo zauważyć, przegrywa z bezwarunkową zdradą. Wniosek z tego, że współpraca ma w darwinowskim świecie pewne szanse.
Od tego czasu pojawiło się wiele nowych modeli matematycznych, które promują strategie związane z kooperacją, czasem nawet bardzo mocno. Powstały między innymi modele z reputacją (pomagaj tym, którzy zyskali reputację, pomagając innym), z aspiracjami (nie zadowalamy się małą wypłatą uzyskiwaną za zdradę zdrajców) czy wreszcie gier przestrzennych z lokalnymi oddziaływaniami. W tym ostatnim modelu wokół współpracującego osobnika tworzy się grupa kooperujących sąsiadów, co wspomaga współpracę, a grupa zdradzających sąsiadów uzyskuje średnio mniejsze wypłaty niż grupa kooperujących altruistów. Modele te zawierają dodatkowe mechanizmy wspomagające kooperację, których nie było w klasycznym „Dylemacie więźnia” i które mogły powstawać drodze ewolucji. Dzięki nim możliwe jest badanie rozwoju pewnych zachowań na bardzo ogólnym, filozoficznym (albo, jak kto woli, matematycznym) poziomie. Badania modeli ewolucyjnych w przeważającej większości nie są powiązane z danymi biologicznymi, społecznymi czy też eksperymentami psychologicznymi. Przyjęte w grze arbitralne wypłaty (np. 5, 3, 1, 0 w „Dylemacie więźnia”) nie mają odniesienia do rzeczywistości. Teoria gier może jednak nabrać charakteru nauki przyrodniczej lub społecznej, gdy wysokość wypłat skalibrujemy na podstawie danych doświadczalnych.
Innym interesującym zastosowaniem gier ewolucyjnych jest badanie możliwości wprowadzenia mechanizmów promujących kooperację do projektowania prawa i funkcjonowania instytucji publicznych. W dylemacie eksploatacji wspólnych zasobów znanym po polsku jako „Tragedia wspólnego pastwiska” (ang. Tragedy of Commons) strategią rolników jest liczba wypasanych krów.
Dla każdego z graczy najlepszą strategią, niezależnie od strategii przyjętych przez innych graczy, jest wypasanie jak największej liczby krów. Takie zachowanie doprowadza do równowagi Nasha, w której wypłata graczy (dzienna ilość mleka) ze względu na degradację pastwiska nie jest wcale maksymalna. Jeżeli jednak odpowiednio opodatkujemy wypasanie maksymalnej liczby krów (zmienimy macierz wypłat gry), to okaże się, że w zmodyfikowanej grze zmieniona równowaga Nasha zapewni wszystkim graczom maksymalne wypłaty przy mniejszej liczbie wypasanych krów. Zauważmy, że w takiej sytuacji nikt nie zapłaci podatku.
Powyższą procedurę można określić jako nieautorytarne wymuszanie określonych zachowań. Jednym z zadań instytucji państwowych powinno być wprowadzanie takich regulacji prawnych, aby w naszych grach życiowych równowagi Nasha dawały nam optymalne wypłaty. W ten sposób zniknęłyby dylematy społeczne.
Możliwość wprowadzania takich zmian wydaje się powiązana z pytaniem, czy możemy być lepsi, niż wynika to z teorii ewolucji. Czy kierując swoim zachowaniem, możemy na obecnym etapie rozwoju ograniczyć skutki i przewidywania teorii ewolucji? Czy możemy pokonać ewolucję albo nią sterować? W darwinowskiej teorii ewolucji opisującej powstawanie i zanik gatunków organizmy nie podejmują racjonalnych decyzji, ale po prostu szybciej lub wolniej się rozmnażają. W badaniach zachowań ludzkich trzeba brać pod uwagę wolną wolę, która wpływa na podejmowanie racjonalnych (lub nie) decyzji. Zamiast bezmyślnej replikacji do rozważań powinniśmy włączyć mechanizmy uczenia się. Z tego powodu długoterminowe zachowanie ewolucyjnych modeli biologicznych i społecznych może się diametralnie różnić.
A w jaki sposób my, matematycy, możemy rozwijać teorię gier i brać udział w powyższych fundamentalnych dyskusjach? Modele teorii gier ewolucyjnych to układy dynamiczne, w których stan populacji graczy zmienia się według ściśle określonych reguł. Na przykład zawody Axelroda można opisać układem równań różniczkowych tzw. dynamiki replikatorowej, które opisują czasową ewolucję częstości występowania poszczególnych strategii. Szybkość zmiany częstości danej strategii jest proporcjonalna do różnicy średniej wypłaty tej strategii i średniej wypłaty w całej populacji. Tu znowu odzywa się Darwin: jeśli wypłata danej strategii jest większa od średniej w populacji, jej częstość występowania rośnie. W przypadku „Dylematu więźnia” sytuacja jest oczywista. Niezależnie od warunków początkowych (z wyjątkiem populacji samych altruistów) populacja bardzo szybko zostanie zdominowana przez zdrajców. W innych, bardziej skomplikowanych modelach o większej liczbie strategii (np. „wet za wet”) albo o innych regułach dynamicznych (np. opierających się na imitacji strategii przeciwnika) zadaniem matematyków jest zbadanie właściwości takich układów. Szukamy odpowiedzi na następujące pytania: w jakich klasach modeli i dla jakich parametrów stany stacjonarne (takie, które nie podlegają dalszej ewolucji) są równowagami Nasha? Czy są one stabilne, tzn. czy po odchyleniu od stanu stacjonarnego układ do niego powróci? Czy możliwe są zachowania cykliczne? Czy dochodzi do wymierania pewnych strategii? Czy możliwe jest współistnienie strategii?
Zazwyczaj zakłada się, że wszelkie oddziaływania zachodzą błyskawicznie, a ich efekty są natychmiastowe. W rzeczywistości w procesach ewolucyjnych wypłaty, czyli zmiany przystosowania (z ang. fitness), pojawiają się z pewnym opóźnieniem. W interakcjach społecznych ludzie podejmują decyzje na podstawie informacji o zdarzeniach, które zaszły w przeszłości. Opóźnienia czasowe mogą powodować oscylacje wokół punktów równowagi.
Rozważmy dynamikę replikatorową z asymptotycznie stabilną równowagą opisującą współistnienie kooperacji i zdrady w grze „Zamieć śnieżna”.
Wyobraźmy sobie dwóch podróżnych, którzy nie mogą kontynuować jazdy samochodem z powodu zatoru śnieżnego na drodze. Niech koszt odśnieżenia wynosi 2, a nagroda (czyli dojazd do domu) to 4. Każdy z graczy może albo kooperować, czyli odśnieżać, albo czekać, aż drugi kierowca odśnieży drogę. Macierz wypłat gry jest wtedy dana przez
| K | Z | |
| K | 3 | 2 |
| Z | 4 | 0 |
W tej grze najlepszą odpowiedzią na kooperację jest zdrada i najlepszą odpowiedzią na zdradę jest kooperacja. Wykazaliśmy, że jeżeli w modelach typu społecznego gracze reagują na informację o wcześniejszym stanie układu z opóźnieniem, to przy odpowiednio dużych opóźnieniach pojawić się mogą oscylacje wokół położenia równowagi.
Z kolei w modelach typu biologicznego, w których wydarzenia z przeszłości wpływają na zmianę przystosowania w teraźniejszości, współistnienie obu strategii jest stabilne dla każdego opóźnienia czasowego. Zbadanie stabilności równowag i powstawanie cykli w matematycznych modelach dylematów społecznych jest niezwykle ważnym kierunkiem badań.
Trzecim nieodłącznym składnikiem teorii ewolucji (oprócz wspomnianej już selekcji i dziedziczenia) są przypadkowe mutacje. Aby je uwzględnić, wprowadzamy do równań element losowy (stochastyczny). Obiektem naszych badań stają się wtedy procesy stochastyczne, w najprostszym przypadku tzw. łańcuchy Markowa, w których prawdopodobieństwo, że badany układ przyjmie określony stan, zależy od jego stanu w chwili bezpośrednio poprzedzającej dany moment, a nie od całej historii układu. Pytamy wtedy, jak zmieniają się i do czego dążą prawdopodobieństwa znalezienia się układu w poszczególnych stanach oraz jakie jest prawdopodobieństwo występowania kooperacji w długookresowym horyzoncie czasowym. Okazuje się, że bardzo często to właśnie zdrada jest stochastycznie stabilna. I znowu szukamy dodatkowych mechanizmów podtrzymujących współpracę, tym razem w świecie niepewnym, podlegającym stochastycznym fluktuacjom.
Jak już wspomnieliśmy, kooperacji może sprzyjać określone rozmieszczenie graczy w przestrzeni. W grach przestrzennych to ułożenie definiujemy poprzez umieszczenie graczy na wierzchołkach grafów tworzących tzw. sieci społeczne. W tym przypadku gracze grają w gry dwuosobowe z najbliższymi sąsiadami, a ich wypłaty są sumą wypłat z poszczególnych gier.
Najnowsze badania wykazały, że grafem szczególnie sprzyjającym kooperacji jest graf Barabási-Alberty.
Powstaje on w następujący sposób. Do wierzchołków już istniejących w każdym kolejnym kroku dodajemy jeden wierzchołek, który łączymy krawędzią z jednym z już istniejących. To, do którego wierzchołka zostanie dołączony, zależy od liczby wychodzących z niego krawędzi. Taka metoda preferencyjnego dodawania nowych połączeń powoduje, że wierzchołki popularne staję się jeszcze bardziej popularne. Gracze umieszczeni w wierzchołkach grafu po uzyskaniu wypłat przyglądają się swoim sąsiadom i naśladują osobnika, który uzyskał najlepszą strategię w poprzedniej rundzie, natomiast z małym prawdopodobieństwem wybierają gorszą strategię.
W „Dylemacie więźnia” rozgrywanym w powyższy sposób po odpowiednio dużej liczbie rund prawie wszyscy osobnicy kooperują. Bardzo dużą funkcję w umacnianiu kooperacji pełnią wierzchołki o bardzo dużej liczbie połączeń, tzw. huby. Wprowadzając do powyższej dynamiki stały koszt utrzymywania połączenia między sąsiadami za pomocą symulacji komputerowych można pokazać, że dla odpowiednio małych kosztów prawie wszyscy kooperują oraz że istnieje koszt krytyczny, dla którego populacja dramatycznie obniża poziom kooperacji do 20%. Dalszy wzrost kosztów nie powoduje dodatkowego obniżenia kooperacji. Co więcej, dla kosztu krytycznego populacja oscyluje pomiędzy 20 a 100% współpracujących osobników. Jest to zjawisko znane z fizyki statystycznej, badającej wiele oddziałujących cząstek – w temperaturze krytycznej układ może znajdywać się w dwóch fazach, czego typowym przykładem jest współistnienie wody i lodu w temp. 0 °C.
Analiza matematyczna przejść fazowych układów społecznych jest bardzo intensywnie rozwijanym kierunkiem badań, prowadzonych również przez autora niniejszego opracowania. Wyciągając wnioski ze skonstruowanych przez siebie modeli, matematycy pokazują, jakie światy są możliwe. W przybliżaniu się do odpowiedzi na pytania, jaka jest nasza rzeczywistość, dlaczego występują w niej zachowania altruistyczne i jak je wzmocnić dla dobra ogółu, niezbędna jest interdyscyplinarna współpraca matematyków z biologami i badaczami zjawisk społecznych.
Jacek Miękisz, profesor nauk matematycznych
Artykuł pierwotnie był opublikowany w czasopiśmie Academia. Magazyn Polskiej Akademii Nauki (1/2016).
Polecamy artykuły „Polowanie na jelenia i równowagi Nasha” oraz „Być albo nie być altruistą – dylemat więźnia” autorstwa prof. Miękisza dostępne na stronie internetowej miesięcznika Delta oraz artykuł „Dylemat więźnia a ewolucja” (Wiedza i Życie, 2/2009), którego kopia jest udostępniona na stronie Autora.