W 1852 roku Francis Guthrie (wówczas student University College w Londynie) zamęczał siebie i swego brata Fredericka pytaniem, czy czterema kolorami można tak pomalować państwa na mapie, aby kraje sąsiednie miały odmienne barwy. Ale problem przerastał również braciszka, więc Francis zainteresował nim swojego profesora matematyki. A był nim nie byle kto, bo August de Morgan, znany szkolnej braci z praw buszujących w logice i zbiorach. Mistrz de Morgan nie potrafił dowieść hipotezy. Ale wykazał, że trzy barwy to co nieco za mało.

W 1878 r. matematyk angielski Arthur Cayley, który też potknął się na tym kolorowym kłopocie, przekazał go Londyńskiemu Towarzystwu Matematycznemu i sprawa nabrała rozgłosu. Problem czterech barw był atakowany z lewa, prawa i którejkolwiek strony się dało. Bez sukcesu. Osiągnięto za to, o dziwo, rozwiązania dla powierzchni wielokroć bardziej skomplikowanych niż swojska płaszczyzna. I tak Percy John Heawood udowodnił w 1890 r. wzór na liczbę koniecznych kolorów w zależności od charakterystyki powierzchni. Np. na torusie – czyli matematycznym obwarzanku (albo dętce) – potrzeba aż siedmiu barw!
Ogólna zasada jest taka: jeśli w powierzchni są dziury (takie jak np. w preclu), to liczba kolorów wzrasta wraz z liczbą dziur. Heawood wykazał, że do pokolorowania mapy na preclu z k dziurami przy k ≧ 1 potrzeba n kolorów, gdzie \({n} =\left\lbrack \frac{1}{2}(7 + \sqrt{1 + 48k}) \right\rbrack,\) przy czym [x] oznacza część całkowitą liczby x.
Łatwo obliczyć, że precel z dwiema dziurami wymaga 8 kolorów, zaś z trzema dziurami już 9.
Zauważmy, że dla k = 0, mamy n = 4 (trudno jednak mówić wówczas o preclu).
*
Pierwszy „dowód” twierdzenia o czterech barwach pojawił się dopiero w roku 1879 w American Journal of Mathematics. Przedstawił go Alfred Bray Kempe, londyński prawnik. Za swoje osiągnięcie Kempe został członkiem Royal Society.
Jak się niezadługo okazało, był to chyba najsłynniejszy fałszywy „dowód” w historii matematyki. Bo 11 lat później wspomniany matematyk brytyjski Percy J. Heawood ujawnił istotny błąd – na domiar złego nieusuwalny – w dowodzie Kempe’a. Twierdzenie znów wróciło na półkę hipotez na niemal cały wiek.
Kiedy duet amerykańskich matematyków Kenneth Appel – Wolfgang Haken ogłosił w 1976 roku swój, ujmując to oględnie, siermiężny komputerowy dowód, świat matematyczny powitał go z oziębłym grymasem. Powód? Miast fajerwerku inwencji, żmudna orka na ugorze polotu, czyli komputerowa analiza wszystkich około dwóch tysięcy szczególnych przypadków, ciurkiem jeden za drugim przez 1200 (słownie: tysiąc dwieście) godzin.
Kontrowersyjny dowód to tasiemcowy wydruk na komputerowe słowo honoru, zaś jego poprawność mógł praktycznie sprawdzić tylko … inny arcysprawny „idiota” (w 2004 udało się to potwierdzić przy użyciu komputerowego „asystenta”). Pomijając oczywiste pytanie; dla kogo właściwie był ten dowód – człowieka czy maszyny – spora część matematyków uważała, że komputer „posunął się” dalece za daleko, obrażając wręcz ich zawodową godność. A przecież już humorysta Tristan Bernard (1866 – 1947) mawiał: „Trzeba wiedzieć, jak daleko można posunąć się za daleko”.
Z tych powodów część matematyków przegnałaby tę metodę dowodzenia na cztery wiatry, a sam corpus delicti zamknęła na cztery spusty w lochu zapomnienia. Znaleźli się jednak i tacy, którzy utrzymywali, że dokonał się tu spektakularny mariaż ludzkiej inteligencji z co prawda debilnym, ale szybkim komputerem.
Reasumując, dowód twierdzenia o czterech barwach był pierwszym spektakularnym osiągnięciem matematyki komputerowej w samej matematyce. Jeśli na początku wzbudzał wiele kontrowersji i mieszane uczucia, to został ostatecznie uznany przez świat matematyczny.
Precedens zatem zaistniał; komputerom zostały na oścież uchylone drzwi do matematyki i, rzecz oczywista, znalazła się spora liczba amatorów zmuszania komputerów do jej „uprawiania”. Tym samym narodził się nowy sposób dowodzenia twierdzeń: tzw. computer-added lub computer-assisted proofs (dowody z asystą komputerową), w których komputerowy asystent był „chłopcem” od obliczeniowej czarnej roboty.
*
Pod koniec XIX wieku postęp w fizyce i matematyce sprawił, że problem prognoz pogody wydawał się być bliskim rozwiązania na wyciągnięcie ręki. Jedyną przeszkodą okazywała się ogromna liczba obliczeń, których wymagało takie zadanie.. Nadzieje odżyły wraz z pojawieniem się komputerów. A jednak prognozowa plajta nadal trwała. W 1963 roku matematyk i meteorolog, Edward Lorenz, usiłując zrozumieć, dlaczego prognozy pogody z reguły zawodzą, odkrył zjawisko zwane deterministycznym chaosem. Kluczem okazał się tzw. efekt motyla, czyli nader wrażliwa zależność od warunków początkowych. Wyjaśniało to czemu numeryczne prognozy pogody nie mogą być „hop-siup”, nawet dla szybkich komputerów.
Istnienie chaosu w równaniach Lorenza rozstrzygnęli w roku 1995 Marian Mrozek (Instytut Informatyki UJ) oraz Konstantin Mischaikow (Georgia Institute of Technology, Atlanta) w pracy Chaos in the Lorenz equations: a computer-assisted proof publikowanej w Bulletin of the American Mathematical Society. Ich wynik Encyclopedia Britannica uznała za jedno z największych na świecie osiągnięć matematyki w 1995 roku.
W pierwotnej wersji dowód wymagał około 80 godzin komputerowych obliczeń (dziś dzięki szybszym komputerom daje się to zrobić w parę minut).
Warto dodać, że w 1999 roku Warwick Tucker w swojej pracy doktorskiej wzmocnił wynik Mrozka i Mischaikowa podając komputerowo wspierany dowód chaotyczności atraktora w równaniach Lorenza.
*
Problem trójek pitagorejskich to pytanie, czy liczby całkowite dodatnie da się pokolorować na czerwono i niebiesko w taki sposób, aby żadna trójka pitagorejska nie składała się tylko z czerwonych lub niebieskich elementów. Innymi słowy, czy możliwe jest pokolorowanie tych liczb na czerwono lub niebiesko w taki sposób, aby dla żadnej trójki liczb całkowitych a, b, c, spełniających równanie a2 + b2 = c2, wszystkie trzy liczby nie były tego samego koloru.
Na przykład w trójce 3, 4 i 5 (odpowiadającej równości 32 + 42 = 52), jeśli 3 oraz 4 są pokolorowane na czerwono, to 5 musi być pokolorowane na niebiesko.
Marijn Heule (University of Texas at Austin), Oliver Kullmann (Swansea University) oraz Victor Marek (University of Kentucky) rozwiązali problem trójek pitagorejskich w 2016 roku, podając dowód wspomagany komputerowo. Zaprzęgli oni do roboty superkomputer, który analizował wszystkie możliwe kombinacji kolorowania liczb. Okazało się, że do liczby aż (lub tylko) 7824 możliwe jest takie kolorowanie liczb, by tworzone z nich trójki pitagorejskie były dwubarwne. Jednak już od 7825 co najmniej jedna trójka pitagorejska miała wszystkie liczby w tym samym kolorze.
Zadanie było niewykonalne dla człowieka, nawet superkomputer miał z nim poważne problemy. By rozwiązać je w rozsądnym czasie, naukowcy ograniczyli liczbę możliwych kombinacji do biliona. Mimo to korzystający z 800 procesorów komputer pracował nad rozwiązaniem przez 48 godzin.
Wyniki te zostały następnie zweryfikowane za pomocą innego oprogramowania, które je potwierdziło. Samo tworzenie dowodu zajęło około 4 lat obliczeń, pracy procesora w ciągu dwóch dni na superkomputerze Stampede (Texas Advanced Computing Center) i wygenerowało aż 200-terabajtowy dowód (skompresowany do 68 gigabajtów w formie listy użytych podprzypadków; 1 terabajt = 1012 bajtów, 1 gigabajt = 109 bajtów).
*
W roku 2010 otrzymano dowód (z asystą komputerową) na optymalne rozwiązanie sławnej kostki Rubika. Otóż można je uzyskać wykonując maksymalnie 20 ruchów ścianką. Ustalono zatem tzw. God’s Number (liczbę Boga). Wynik zawdzięczamy pracy Tomasa Rokickiego, Herberta Kociemby, Morleya Davidsona i Johna Dethridge’a.
*
W 2012 roku tercet Gary McGuire (University College Dublin) i jego współpracownicy – Bastian Tugemann i Giles Civario – wykazali (a właściwie potwierdzili dzięki czarnej robocie komputerowego asystenta), że 17 to minimalna liczba informacji (wskazówek) potrzebna do rozwiązania każdej unikalnej, a więc jednoznacznej w rozwiązaniu, łamigłówki sudoku. Warto nadmienić, że algorytm sprawdzający sudoku, opracowany przez owe trio z irlandzkiego uniwersytetu, znalazł swoje praktyczne zastosowania w bioinformatyce i sieciach telefonii komórkowej.
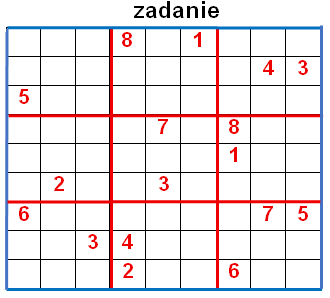
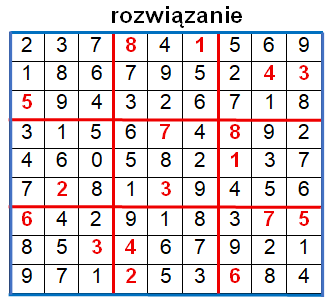
Tym wszystkim, którym nazwa sudoku mówi niewiele lub zgoła nic, wyjaśniamy: to łamigłówka powszechnie uważana za japońską (choć w istocie wymyślona została przez matematyka ze Szwajcarii), w której należy wpisać liczby od 1 do 9 w taki sposób, aby nie powtarzały się ani w żadnej kolumnie (pionie), ani w żadnym wierszu (poziomie). Cała plansza sudoku składa się z dziewięciu małych kwadratów 3x3, w których należy wpisać brakujące liczby od 1 do 9 (każdą jeden raz w każdy kwadrat).
Oto przykładowe sudoku wraz z jego rozwiązaniem.
Jest wiele powodów czyniących sudoku grą wartą zachodu; powszechnie dostępna (prasa, internet) intelektualna zabawa wraz z ćwiczeniem szarych komórek – pomaga w walce z demencją i odwraca uwagę mózgu od stresu i zmęczenia (zalecana przez lekarzy i trenerów celem utrzymania elastyczności umysłu). I co równie ważne, to łamigłówka w pełni uniwersalna – nie liczy się płeć, język ani wiek (może poza niemowlętami).. Liczą się wyłącznie liczby. Ponadto wiele aplikacji umożliwia wybór poziomu trudności, podpowiedzi czy możliwość sprawdzania poprawności rozwiązania.
Od 2006 roku odbywają się coroczne Mistrzostwa Świata w Sudoku, a pochodzący z Krakowa Jan Mrozowski był trzykrotnym mistrzem świata w tej grze (World Sudoku Championship w 2009, 2010 i 2012).
Wracając do komputerowych dowodów nadmieńmy, że mnożą się one niczym grzyby po deszczu, a ich liczba od czasów wyczynu spółki Appel – Haken stale pnie się w górę w coraz szybszym tempie. A pól wieku po ich wyczynie np. Uniwersytet Jagielloński uruchomił matematykę komputerową – kierunek studiów, zwany również matematyką obliczeniową (ang. computational mathematics) – mariaż matematyki z informatyką. A tych, którzy pragną więcej przykładów, informujemy, że Wikipedia zamieszcza listę Theorems proved with the help of computer programs (Twierdzenia udowodnione przy pomocy programów komputerowych).
Skoro o komputerowych dowodach mowa, warto wspomnieć o oryginalnym pomyśle szkockiego start-upu TheoryMine (Twierdzeniowa kopalnia), założonego przez naukowców School of Informatics, the University of Edinburgh w 2009 roku. Specjalnością firmy była automatyzacja dowodów dzięki AI (Artificial Intelligence), Na życzenie klienta generowała nowe twierdzenie z algebry, a za cenę 15 funtów można było nazwać je wybranym imieniem i otrzymać efektowny certyfikat z dołączonym dowodem potwierdzającym, że dane twierdzenie jest prawdziwe.
Wszyscy ci, którzy chcieliby zaszpanować w towarzystwie swoim „matematycznym talentem”, wzbudzając uznanie i podziw dzięki twierdzeniu nazwanemu na cześć swojego imienia (pomijając dyskretnym milczeniem, że uzyskanego przez „dowód z obwodu”), muszą dziś obejść się smakiem, bowiem w roku 2019 start-up TheoryMine zakończył działalność.
Tadeusz Ostrowski
dr nauk matematycznych