Różne oblicza symetrii. Odcinek 8

Część XIV. Źró­dła i pod­pa­trze­nia (3)

Lustro… Lustro w lite­ra­tu­rze ma mnó­stwo zasto­so­wań i wła­sno­ści. Jeśli jesz­cze w tle poja­wia się mate­ma­ty­ka, sko­ja­rze­niem dość oczy­wi­stym jest Ali­cja w kra­inie cza­rów. Ale to lustro mnie roz­cza­ro­wu­je – jest spro­wa­dzo­ne do roli bło­ny, barie­ry lub bra­my do… Może lep­sza sta­ra szafa?

O wie­le cie­kaw­sze jest lustro w książ­ce Fyn­na Halo, pan Bóg? Tu Anna… (W dro­dze, 1994). Rzecz jest o nie­zwy­kłej kil­ku­let­niej dziew­czyn­ce prze­ni­kli­wie widzą­cej pro­ble­my egzy­sten­cjal­ne, pro­wa­dzą­cej swo­isty dia­log z Bogiem, rozu­mie­ją­cej cel ist­nie­nia. Czytelnika-matematyka może zain­te­re­so­wać w tej książ­ce opis wręcz badaw­czej obser­wa­cji lustra, a raczej pary luster. Zadzi­wia gład­kie przej­ście od trój­ką­ta, przez czwo­ro­kąt, pię­cio­kąt itd., aż do okrę­gu, któ­ry rap­tem sta­je się „naj­więk­szym kołem świa­ta”, a póź­niej wygi­na się w dru­gą stro­nę. A do tego potrzeb­ne były tyl­ko dwa luster­ka spo­ty­ka­ją­ce się pod róż­ny­mi kąta­mi… Mamy do czy­nie­nia z wie­lo­krot­nym zło­że­niem dwóch symetrii.

Nie chcę zdra­dzać wszyst­kie­go. War­to prze­czy­tać same­mu. Moż­na być pod wra­że­niem intu­icji auto­ra lub – jeśli nie była zmy­ślo­na – małej Anny, intu­icji ogar­nia­ją­cej nie­skoń­czo­ność aż po kres, a raczej po ciąg dal­szy za punk­tem w nie­skoń­czo­no­ści (takie mam wywo­dzą­ce się z geo­me­trii rzu­to­wej sko­ja­rze­nia). Na wszel­ki wypa­dek: ksią­żecz­ka nie wyma­ga od Czy­tel­ni­ka żad­nej spe­cja­li­stycz­nej wie­dzy i może zacie­ka­wić każdego.

Od daw­na mój wzrok przy­cią­ga­ją orna­men­ty, już o tym wspo­mi­na­łem. 30 lat temu zaglą­da­łem czę­sto do książ­ki Rudol­fa Kut­zlie­go Lan­go­bar­di­sche Kunst. Die Spra­che der Flecht­bän­der (Ura­ch­haus, 1986) ana­li­zu­ją­cej sztu­kę Longobardów.

Wcią­ga­ło mnie stu­dio­wa­nie foto­gra­fii zdo­bień romań­skich kościo­łów i innych kamien­nych obiek­tów powsta­łych w cza­sach, gdy na pół­no­cy Pół­wy­spu Ape­niń­skie­go miesz­ka­li Lon­go­bar­do­wie (czy­li ci mają­cy dłu­gie bro­dy), zwa­ni też Lom­bar­da­mi, po nich zosta­ła nazwa regio­nu: Lom­bar­dia. Mister­ne prze­pla­ta­ją­ce się linie to moty­wy, któ­re dziś koja­rzy­my raczej ze sztu­ką cel­tyc­ką. Nie­któ­re są wręcz iden­tycz­ne ze spo­ty­ka­ny­mi w Irlan­dii i w Szko­cji wzo­ra­mi. Książ­ki nie zgłę­bi­łem do koń­ca, po pro­stu nie znam języ­ka niemieckiego.

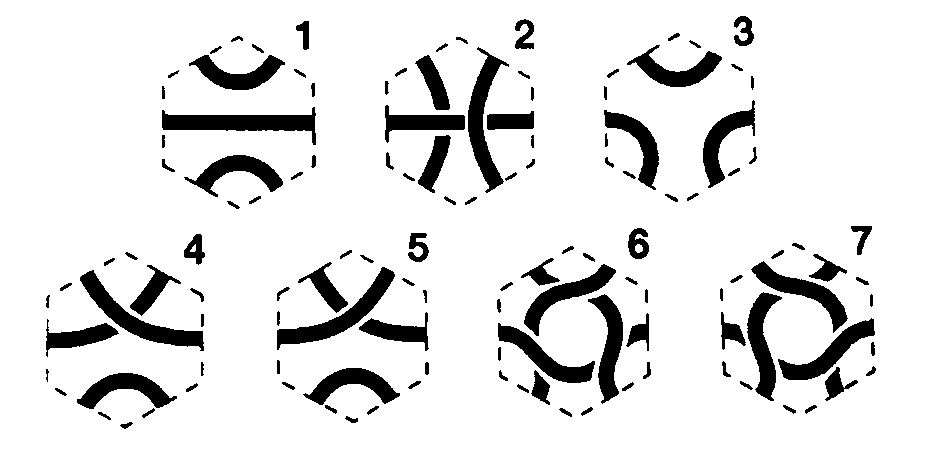
Mniej wię­cej w tym samym cza­sie widzia­łem po raz pierw­szy Tiling Gene­ra­tors sto­so­wa­ne w bry­tyj­skich szko­łach. To były tek­tu­ro­we płyt­ki: kwa­dra­ty lub sze­ścio­ką­ty forem­ne, wszyst­kie z boka­mi tej samej dłu­go­ści, któ­re na bia­łym tle mia­ły nadru­ko­wa­ne linie. Angiel­skie płyt­ki mia­ły tyl­ko jeden wzór gra­ficz­ny na każ­dym sze­ścio­ką­cie (na ilu­stra­cji wzór nr 1) i tyl­ko jeden na kwa­dra­cie (na ilu­stra­cji po lewej).

Po powro­cie do Pol­ski bawi­łem się tymi kar­to­ni­ka­mi i uzna­łem, że war­to angiel­skie kom­ple­ty uzu­peł­nić nowy­mi typa­mi pły­tek. Doda­łem jeden wzór na kwa­dra­cie i sześć wzo­rów na sześciokącie.

W ten spo­sób powsta­ły Ukła­dan­ki nie­skoń­czo­ne. Z moich pły­tek daje się uło­żyć wie­le cel­tyc­kich wzorów.

Część XV. Źró­dła i pod­pa­trze­nia (4)

Ency­klo­pe­dia szkol­na. Mate­ma­ty­ka (WSiP, 1988) to publi­ka­cja, w któ­rej róż­nym rodza­jom syme­trii poświę­co­no dużo miej­sca i uwa­gi. W oddziel­nych hasłach (syme­tria, syme­tria osio­wa, syme­tria płasz­czy­zno­wa, syme­tria środ­ko­wa, syme­tria z obro­tem, syme­tria z pośli­zgiem) omó­wio­ne są poszcze­gól­ne prze­kształ­ce­nia w uję­ciu syn­te­tycz­nym i w uję­ciu ana­li­tycz­nym. Wspo­mnia­na jest też syme­tria obro­to­wa. Jako wpro­wa­dze­nie w świat defi­ni­cji pojęć ency­klo­pe­dia nada­je się świet­ne. Bra­ku­je w niej nie­co mate­ria­łu dają­ce­go opar­cie intu­icji. Ale w ency­klo­pe­diach na ogół nie ma na to miej­sca. Opi­sa­ne tam poję­cia mate­ria­li­zu­ją się w świe­cie nas ota­cza­ją­cym i czę­sto gra­ją waż­ną rolę w przy­ro­dzie, sztu­ce, tech­ni­ce itd., ale czę­sto wymy­ka­ją się per­cep­cji jako nie­na­zwa­ne lub zbyt oczywiste…

Pierw­sze kro­ki w odży­wia­niu intu­icji moż­na robić z ksią­żecz­ką Marion Wal­ter The Mir­ror Puz­zle Book (Tarqu­in Publi­ca­tion, 1985). W kom­ple­cie luster­ko słu­żą­ce do takie­go przy­kła­da­nia do wyj­ścio­we­go rysun­ku, żeby móc zoba­czyć inne widocz­ne na jed­nej roz­kła­dów­ce obraz­ki. Ale są takie rysun­ki, któ­rych tak uzy­skać się nie da. Dla dzie­ci? Tak, ale… Nie wszyst­kim doro­słym dobrze idą zma­ga­nia z tymi zagadkami.

Dla star­szych, bar­dziej serio: Krzysz­to­fa Mostow­skie­go i Wacła­wa Zawa­dow­skie­go Geo­me­tria. Mate­ma­ty­ka dla nauczy­cie­li (Wydaw­nic­two Nowik, 2020). Oprócz wie­lu smacz­nych dro­bia­zgów jest tu dobrze potrak­to­wa­na syme­tria obro­to­wa. Cie­ka­wy jest pomysł na potrak­to­wa­nie tej syme­trii jako przekształcenia.

Przy oka­zji – syme­tria w mate­ma­ty­ce może być trak­to­wa­na jako wła­sność lub jako prze­kształ­ce­nie. Dopie­ro teraz o tym piszę, ale war­to to cza­sem odróż­nić. Zaraz o tym zapo­mnę, jestem jed­nak spo­koj­ny: to kon­tekst czy­ni zna­cze­nie. Czy zga­dzasz się, Czytelniku?

Kolej­ny sto­pień zaawan­so­wa­nia to Roge­ra G. New­to­na Zro­zu­mieć przy­ro­dę (Pró­szyń­ski i S‑ka, 1996). Spo­ro jest tu o syme­trii. Naj­pierw frag­ment, któ­ry spra­wia wra­że­nie stresz­cze­nia książ­ki Wey­la, nawet poja­wia­ją się te same ilu­stra­cje. W roz­dzia­le Pięk­no i potę­ga syme­trii jest też co inne­go – wspo­mnie­nie o kano­nach Bacha (czę­sto sto­so­wał syme­trię lustrza­ną, prze­su­nię­cia są w muzy­ce sta­le obec­ne i koniecz­ne), o syme­trii w fizy­ce, o zasa­dach zacho­wa­nia, o syme­triach w mecha­ni­ce kwan­to­wej… Może poznam kie­dyś cie­ka­we wyja­śnie­nia fizyka.

Pro­fe­sor Jan Mozrzy­mas, mate­ma­tyk, orga­ni­zo­wał we Wro­cła­wiu inter­dy­scy­pli­nar­ne semi­na­ria doty­czą­ce syme­trii. Mam dwie ksią­żecz­ki, któ­re powsta­ły w związ­ku z tymi stu­dia­mi – Jana Mozrzy­ma­sa i Andrze­ja Wolań­skie­go Har­mo­nia sfer nie­bie­skich i muzy­ka abs­trak­cyj­nych syme­trii oraz pra­cę zbio­ro­wą Syme­trie w sztu­ce i naukach huma­ni­stycz­nych. Jak tajem­ni­czo brzmią tytu­ły roz­dzia­łów: „O pro­por­cjach i syme­trii Wstę­pu do pierw­sze­go aktu ope­ry Lohen­grin Ryszar­da Wagne­ra” albo „Odnaj­dy­wa­nie syme­trii jako dyrek­ty­wa meto­do­lo­gicz­na w bada­niach socjo­lo­gicz­nych”? Obie książ­ki zosta­ły wyda­ne przez Uni­wer­sy­tet Wro­cław­ski. Są to więc dale­kie wypra­wy poza samą mate­ma­ty­kę. Nie zali­czał­bym tych ksią­żek do łatwej lektury.

Jan Bara­now­ski

Zdję­cia i gra­fi­ki zosta­ły przy­go­to­wa­ne przez auto­ra artykułu.