Ian Stewart
Gabinet matematycznych zagadek. Część II
Wydawnictwo Literackie. Kraków 2012
Jeśli ktoś miał już okazję poznać książkę Gabinet matematycznych zagadek autorstwa Iana Stewarta (recenzja dostępna jest tutaj) i polubił rozwiązywanie łamigłówek oraz odkrywanie matematycznych ciekawostek, to na pewno z ogromną przyjemnością sięgnie także po kontynuację. Część II posiada wszystkie atuty poprzedniej części.
Dodajmy, że – wbrew temu, co może zasugerować polski tytuł – autor nie zaplanował Gabinetu w dwóch częściach. Ian Stewart we wstępie opowiada o tym, jak po ogromnym sukcesie pierwszej książki – został poproszony o napisanie kontynuacji. Jej oryginalny tytuł to „Professor Stewart’s Hoard of Mathematical Treasures”, co można przetłumaczyć dosłownie jako „Skarbiec matematycznych skarbów profesora Stewarta”. Polski wydawca zdecydował się na tytuł „Gabinet matematycznych zagadek. Część II”.
Na język polski książkę przełożyła Agnieszka Sobolewska (autorka przekładu części I). Konsultantem polskiego wydania był Stefan Turnau1.
***
Skoro najlepsze zagadki oraz najbardziej popularne tematy pojawiły się już w części I (autor pisze: „Nieco mniej [miejsca poświęciłem] natomiast wielkim problemom czystej matematyki, głównie dlatego, że w Gabinecie omówiłem kilka tych naprawdę smakowitych.”) , to czy siłą rzeczy część II jest gorsza? Otóż nie, gdyż autor znalazł kolejne ciekawe tematy do przedstawienia – kilka z nich przywołuję w tej recenzji. Doświadczony miłośnik matematyki powinien więc znaleźć tu więcej nowości, tym razem w postaci mniej znanych ciekawostek.
Zagadki kończą się odnośnikiem do rozwiązania: „Odpowiedź na stronie x”, który odsyła nas do… Dokąd? Zacytuję autora książki:
Specjalny składzik sprytnych rozwiązań i stymulujących suplementów profesora Stewarta …gdzie dociekliwy lub zdeprymowany czytelnik znajdzie odpowiedzi na te pytania, które według obecnego stanu wiedzy odpowiedzi posiadają… oraz, nieodpłatnie, garść faktów i fantazji gwoli dalszej przyjemności, jak i oświecenia.
Odpowiedzi zajmują czasem nawet cztery strony.
Jednak i ci, którzy nie przepadają za rozwiązywaniem zagadek, znajdą w książce coś dla siebie. We wstępie profesor Stewart pisze:
Kiedy grzebałem w moim archiwum, wybierając nowe materiały do Gabinetu, podzieliłem – na własny użytek – jego zawartość według różnych kategorii: zagadki, gry, modne słówka, humoreski, najczęściej zadawane pytania, anegdoty, wyliczanki, niesamowitości, faktoidy (niesprawdzone informacje spopularyzowane przez media), żarty, ciekawostki, paradoksy, folklor, tajemnice itd.
Wymienię przykładowe serie oraz zagadnienia (według mojego podziału na kategorie).
Znajdziemy wiele serii obecnych już w pierwszej części. Książkę otwierają Osobliwe obliczenia. Tym razem dostajemy tylko trzy pojedyncze sztuczki, ograniczające się do „magicznego” mnożenia. Pojawią się też dwa zadania logiczne (ze zdaniami w rodzaju: „Każde stworzenie jedzące miód potrafi grać na kobzie.”), w których musimy sprawdzić, czy przedstawiona dedukcja jest prawidłowa.
Spotkamy tu również postacie, które pojawiły się już w pierwszej części, a które tym razem utworzą swoje własne miniserie.
To podróż pełna magii – momentami dosłownie – gdyż Wielki Chudyni (wraz ze swoją asystentką Gderliną) pojawia się aż osiem razy. Nietrudno odgadnąć, że inspiracją był Harry Houdini, jeden z najsłynniejszych iluzjonistów i specjalistów od ucieczek wszech czasów. My nie będziemy jednak nigdzie uciekać, charakter tych sztuczek to przede wszystkim tzw. odgadnienia. Polegają one na tym, że jeśli uważnie prześledzimy wykonywane operacje i obliczenia, okaże się, że wynik końcowy wcale nie zależy od początkowo pomyślanej liczby, albo ta liczba jest sprytnie zaszyfrowana w ostatecznym rezultacie.
Zapoznamy się również z historią obliczeń. Jak zapowiada autor:
Wyjaśnię także kilka kwestii historycznych, jak cyfry babilońskie, liczydło i egipskie ułamki. Historia matematyki liczy sobie co najmniej 5000 lat, a odkrycia dokonane w dalekiej przeszłości są do dziś istotne, bo rozwój tej dziedziny opiera się na jej dawnych sukcesach.

źródło: WikiMedia (CC BY-SA 4.0)
I rzeczywiście – możemy przeczytać o Sekretach liczydła; zatrzymać się Nad liczbami Babilonu; odkryć Egipskie ułamki; a także zobaczyć, jak Mnożenie za pomocą linijek prowadzi do logarytmów.
W drugiej części Gabinetu poznamy też zupełnie nowe postacie. Mamy tu nową miniserię, której bohaterem jest kapitan Roger Rudobrody. To seria czterech „pirackich” zadań, w których spróbujemy m.in. znaleźć Skarb Rudobrodego, czy rozwiązać zagadkę Pięciu hiszpańskich dolarów.
Historia matematyki to nie tylko ewolucja systemów liczbowych czy technik obliczeń. Dowiemy się również, skąd wzięły się niektóre symbole, które są obecnie powszechnie stosowane w matematycznej notacji – bo przecież ktoś kiedyś musiał je wymyślić. Te ciekawostki przeczytamy w rozdziałach: Kto wynalazł znak równości? Skąd się wziął symbol pierwiastka kwadratowego, liczby pi oraz silni?
Trafimy też na kilka całkiem poważnych problemów, ale o naprawdę „dziwnie” brzmiących nazwach. Twierdzenie o zaczesaniu sfery mówi nam, że niestety nie da się jej uczesać (cokolwiek miałoby to znaczyć). Rogata sfera Alexandra to taka niesforna sfera, której „obszar zewnętrzny nie jest równoważny topologicznie z obszarem na zewnątrz zwykłej sfery”. Sam opis brzmi dość enigmatycznie – dlatego warto zobaczyć ją na ilustracji.
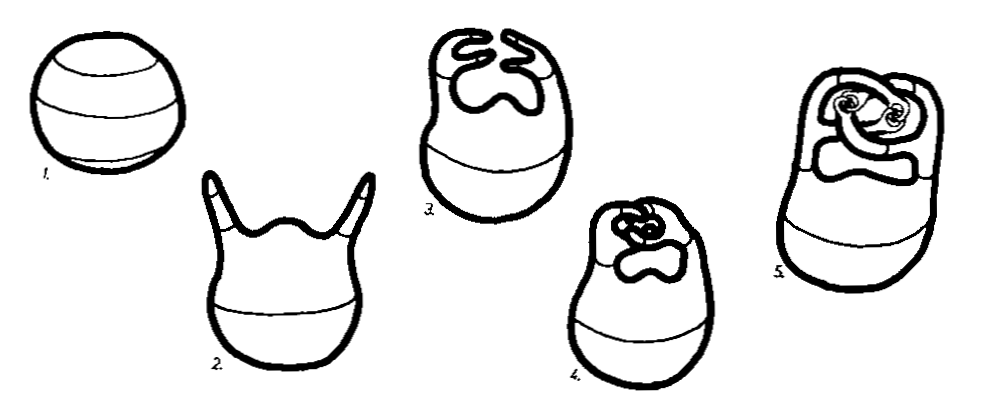
„Każdą z [dwóch] rączek rozszczepiamy na dwie (…) i powstałe odgałęzienia przeplatamy ze sobą. (…) Tę konstrukcję kontynuujemy indukcyjnie. Mając w n‑tym kroku 2n rączek (…) konstruujemy 2n+1 obejmujących się rozgałęzień.”
Rysunek i cytat pochodzą z artykułu K. Ciesielskiego i Z. Pogody z miesięcznika Delta (nr 6 z 1987 r.)
Z kolei Twierdzenie o kanapce z szynką podpowiada, że zawsze istnieje takie cięcie, które podzieli każdy składnik dokładnie na pół (pod względem objętości). Znajdziemy również instrukcję, Jak wywrócić sferę na lewą stronę.
W książce popularnonaukowej nie mogło oczywiście zabraknąć najbardziej znanych tematów matematycznych.
Poczytamy o tym jak powstają – i jak bywają łamane – Tajne szyfry („Zaszyfrowane wiadomości są tak stare jak samo pismo.”). A kiedy już poznamy odpowiedź na pytanie Kiedy 2+2=0? („To arytmetyka modularna, szeroko stosowana w teorii liczb.”), będziemy bardziej gotowi na zaskakujące Tajne szyfry, które można ujawnić publicznie2. Spotkamy także Niekończące się sumy, które „należą do najważniejszych matematycznych wynalazków”. A jeśli ktoś lubi filozoficzne rozważania, to Paradoksalny Zenon z Elei przedstawi nam swoje paradoksy, czyli zbiór „czterech eksperymentów myślowych, z których każdy ma na celu udowodnienie, że ruch jest niemożliwy”. Z kolei Butelka Kleina to „przykład powierzchni bez brzegu i z tylko jedną stroną”. (Czytelnicy pierwszej części „Gabinetu” zapewne pamiętają, że „wstęga Möbiusa ma jedną stronę, ale ma też brzeg”).
Niektóre hasła prowadzą nas do naprawdę wielkich problemów matematycznych i najbardziej znanych zagadnień. Jednym z nich jest Lista przebojów Hilberta. („W 1900 roku niemiecki matematyk David Hilbert wygłosił słynny wykład na Międzynarodowym Kongresie Matematyków w Paryżu, w którym wymienił 23 najważniejsze problemy matematyki.”)
W drugiej części Gabinetu pojawiają się też fragmenty poświęcone samej matematyce (jako dziedzinie nauki). Znajdziemy tu „zbiorcze” hasła z cytatami, które ukazują Matematyków (a także Niematematyków) rozmyślania nad matematyką, a także dowcipne Techniki dowodowe. W książce została też zamieszczona zwięzła i Krótka historia matematyki.
Innumeratus i Matmofila – para bliźniaków znana już z pierwszej części – wraca tutaj ponownie i to aż pięć razy. To swego rodzaju matematyczne wyzwania, które próbują nas zmylić (np. Brakujący kawałek). Bardzo ciekawym (i długim) hasłem jest tajemniczo brzmiące Juniper Green. „-Zagrajmy w grę liczbową – zaproponowała Matmofila. Innumeratus, ten frajer, połknął haczyk”. Jak zakończyła się ta historia? Tego już dowiemy się z lektury.
Nową postacią jest „nieustraszony poszukiwacz przygód i łowca skarbów Colorado Smith”, wraz ze swoją pomocniczką Brunhildą. Opisy towarzyszące tym hasłom przywodzą na myśl filmy o dzielnych archeologach. Trochę szkoda, że autor umieścił w książce tylko dwa zadania z ich udziałem.
Coś dla siebie znajdą także fani (zastosowań matematyki w) astronomii. W części I poznaliśmy już odpowiedź na pytanie Jaki kształt ma sierp Księżyca? Teraz z hasła To tylko taka faza dowiemy się, „kiedy widoczny obszar to dokładnie jedna czwarta powierzchni księżycowej tarczy”?
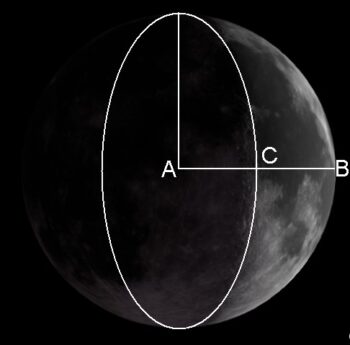
Oba hasła ukazują nam praktyczne zastosowania geometrii w wyjaśnianiu zjawisk, które od tysiącleci przyciągały uwagę człowieka, a które i dziś obserwujemy na niebie.
Poznajemy także odpowiedzi na kolejne dwa z często zadawanych pytań: Dlaczego nie mogę dodawać ułamków tak, jak je mnożę? oraz Ile to jest 0,999…?
***
Druga część Gabinetu matematycznych zagadek Iana Stewarta to kolejne niesamowite wyzwania dla miłośników łamigłówek – nowa porcja niecodziennych zagadek, których rozwiązywanie sprawi sporo przyjemności i satysfakcji.
Książka napisana jest prostym, przystępnym językiem, a lekkość lektury to w dużej mierze zasługa przeplatania zagadek z opowieściami. To nie tylko świetna zabawa pełna ciekawostek – to także podróż przez matematyczny świat, z której wychodzimy bogatsi o nowe doświadczenia i wiedzę. Można by rzec, że kończymy ją z głową pełną „matematycznych skarbów”.
Wydawnictwo Literackie po raz kolejny zadbało o atrakcyjną oprawę graficzną książki (wydanie pierwsze, które recenzuję). Dla porównania – zamieszczam też okładkę drugiego wydania (z 2021 roku).
1Warto wspomnieć, że Stefan Turnau (zmarł w styczniu 2025 roku) był wybitnym dydaktykiem matematyki (dr hab.) oraz autorem i współautorem wielu szkolnych podręczników z matematyki i poradników metodycznych.
2W komentarzu do tego hasła na s. 340, przy opisie procedury RSA, znajduje się drobny błąd w zdaniu: „Wybieramy liczbę całkowitą s (jak szyfrowanie) między 1 a (p – 1)(q – 1), która nie jest wielokrotnością p ani q.”. Poprawny warunek brzmi: s ma być liczbą względnie pierwszą z iloczynem (p – 1)(q – 1).





