Różne oblicza symetrii. Odcinek 9

Część XVI. Źró­dła i pod­pa­trze­nia (5)

Wąt­ki tej czę­ści opo­wie­ści o syme­trii wyma­ga­ją uży­cia nie­co bar­dziej zaawan­so­wa­nych pojęć i ter­mi­nów. Prze­pra­szam więc Czy­tel­ni­ków, któ­rzy zaufa­li mi, że piszę języ­kiem przy­stęp­nym i straw­nym dla tych, któ­rym mate­ma­ty­ka wyż­sza jest zbyt obca. Zale­ży mi jed­nak na poka­za­niu, jak cza­sem wyglą­da­ją roz­wa­ża­nia matematyków.

Się­gam tu do dwóch fun­da­men­tal­nych ksią­żek, któ­re od lat słu­żą mi jako punk­ty odnie­sie­nia. Ich auto­rzy, David Hil­bert (1862–1943) i Harold Scott Mac­Do­nald Coxe­ter (1907–2003), to gigan­ci geometrii.

David Hil­bert, Ste­fan Cohn-Vossen Geo­me­tria poglą­do­wa (PWN 1956) to zna­ko­mi­ta książ­ka napi­sa­na jed­no­cze­śnie języ­kiem ści­słym i swo­bod­nym. Znaj­dzie­my w niej dużo o syme­triach oraz o sie­ciach na płasz­czyź­nie i w prze­strze­ni. Tekst moż­na sma­ko­wać i podzi­wiać sta­ry styl wykła­du, w któ­rym do szu­ka­nych pojęć docho­dzi się powo­li, a grun­tow­nie. W latach 30. XX wie­ku (nie­miec­kie wyda­nie książ­ki pocho­dzi z 1932 r.) nie sądzo­no, że moż­na chwy­cić książ­kę i nie­cier­pli­wie szu­kać kon­kret­nych defi­ni­cji. Od tego cza­su nawet nar­ra­cja ksią­żek aka­de­mic­kich się zmieniła.

Harold Scott Mac­Do­nald Coxe­ter Wstęp do geo­me­trii daw­nej i nowej (PWN 1967) to wykład już w now­szym sty­lu (angiel­skie wyda­nie książ­ki jest z 1961 r.). Znaj­dzie­my tu defi­ni­cje doty­czą­ce syme­trii, z uwzględ­nie­niem ich uję­cia w języ­ku teo­rii grup. Podob­nie jak u Hil­ber­ta i Cohn-Vossena poja­wia­ją się syme­trie obro­to­we i prze­su­nię­cio­we. Wstęp… war­to choć­by prze­kart­ko­wać – to cie­ka­we spoj­rze­nie na geometrię.

Teo­rio­gru­po­we podej­ście do syme­trii stwa­rza moż­li­wość utoż­sa­mie­nia izo­me­trii i symetrii.

Gdy zaczy­na­my zaj­mo­wać się syme­trią, naj­pierw wyda­je się, że to poję­cie w mia­rę dobrze zde­fi­nio­wa­ne, że może słu­żyć jako solid­ny wzór, sza­blon, szkie­let albo nawet krę­go­słup pew­nej czę­ści geometrii.

Ale jak to z krę­go­słu­pem było? (To odci­nek pierw­szy). Może być porażka…

A tym­cza­sem… na praw­dzi­wą nie­spo­dzian­kę natkną­łem się w Co to jest mate­ma­ty­ka? Richar­da Couran­ta i Her­ber­ta Rob­bin­sa (Pró­szyń­ski i S‑ka 1998). Książ­ka ta nie jest mono­gra­fią, lecz (dość potęż­nym) ese­jem o mate­ma­ty­ce. Prze­kształ­ce­nia geo­me­trycz­ne są w książ­ce oma­wia­ne bar­dziej ogól­nie, „z lotu ptaka”.

Otóż według auto­rów inwer­sja płasz­czy­zny wzglę­dem okrę­gu jest uogól­nie­niem „zwy­kłej’’ syme­trii osio­wej (wzglę­dem prostej)!

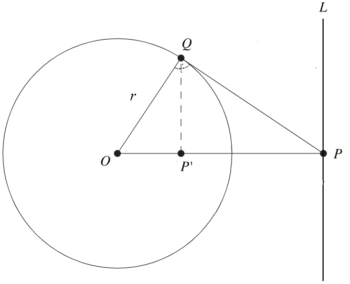
Inwer­sja wzglę­dem okrę­gu o środ­ku O i pro­mie­niu r to takie prze­kształ­ce­nie płasz­czy­zny, któ­re każ­de­mu punk­to­wi P (róż­ne­mu od punk­tu O) przy­po­rząd­ko­wu­je punkt P’ leżą­cy na pół­pro­stej OP, speł­nia­ją­cy waru­nek r² = OP ⋅ OP’.

Obra­zo­wo moż­na to okre­ślić jako „prze­ni­co­wa­nie”, „wywi­nię­cie” płasz­czy­zny – wnę­trze okrę­gu prze­cho­dzi na zewnę­trze i na odwrót, zewnę­trze okrę­gu – na wnętrze.

Inwer­sja nie jest izo­me­trią. Jeśli syme­trię osio­wą nazwie­my odbi­ciem lustrza­nym, to inwer­sja była­by odbi­ciem w bar­dzo krzy­wym zwier­cia­dle. Mimo to zacho­wu­je kąty: to zna­czy kąty mię­dzy pro­sty­mi lub krzy­wy­mi po prze­kształ­ce­niu są takie same jak przed prze­kształ­ce­niem. Obra­zy okrę­gów nie­za­wie­ra­ją­cych środ­ka inwer­sji to inne okrę­gi. Nato­miast obra­za­mi pro­stych są okrę­gi prze­cho­dzą­ce przez śro­dek inwersji.

I oto wra­ca „naj­więk­sze koło świa­ta”, czy­li pro­sta z Halo, Pan Bóg? Tu Anna… (odci­nek ósmy).

Włą­cze­nie inwer­sji do kata­lo­gu syme­trii jest zdu­mie­wa­ją­ce, a jed­no­cze­śnie otwie­ra cie­ka­we perspektywy.

W Nie­zwy­kłych licz­bach pro­fe­so­ra Ste­war­ta Iana Ste­war­ta (Pró­szyń­ski i Ska 2016) pierw­szy raz zwró­ci­łem uwa­gę na zda­nie: „syme­tria to prze­kształ­ce­nie, któ­re zacho­wu­je struk­tu­rę prze­kształ­ca­nej prze­strze­ni”. Ha! Czy­li nie tyl­ko izo­me­trie, ale też podo­bień­stwa i prze­kształ­ce­nia zwę­ża­ją­ce. A gdy odej­dzie­my dalej od prze­strze­ni eukli­de­so­wej – choć­by do prze­strze­ni rzu­to­wej – musi­my usta­lić, o jakiej struk­tu­rze mowa. A co to jest syme­tria na sferze?

Jeśli odrzu­ci­my metry­kę i o struk­tu­rze decy­do­wać będą home­omor­fi­zmy, jak­że cie­ka­we zro­bią się symetrie!

Home­omor­fizm (ter­min topo­lo­gicz­ny) to takie prze­kształ­ce­nie cią­głe, któ­re ma prze­kształ­ce­nie odwrot­ne rów­nież cią­głe. Zwy­kle poda­je się przy­kład kub­ka z uszkiem, któ­ry jest home­omor­ficz­ny z obwa­rzan­kiem; podob­nie powierzch­nia bry­ły wypu­kłej jest home­omor­ficz­na ze sferą.

Z jasne­go i dobrze okre­ślo­ne­go poję­cia robi się nagle coś dziw­ne­go, sprzecz­ne­go z intuicją.

Na począt­ku roku 2021 poja­wi­ła się infor­ma­cja, że trzej pol­scy mate­ma­ty­cy zna­leź­li odpo­wiedź na waż­ne pyta­nie o syme­trie wszyst­kich syme­trii. W inter­ne­to­wym wywia­dzie pro­fe­sor Piotr Nowak – jeden z nich – opo­wia­da, o co w tym cho­dzi. Istot­ne jest to, że auto­mor­fi­zmy są alge­bra­icz­ny­mi syme­tria­mi. Auto­mor­fizm to prze­kształ­ce­nie obiek­tu, któ­re zacho­wu­je jego strukturę.

Naj­le­piej jed­nak, żeby to pro­fe­sor Nowak powie­dział o tym sam:

***

Część XVII. Źró­dła i pod­pa­trze­nia (6)

Pocz­tar­że
Kie­dyś wer­tu­jąc sta­re rocz­ni­ki cza­so­pi­sma „Mate­ma­ty­ka”, natkną­łem się na wybra­ne przez Jana Ziem­bę zada­nia ze sta­rej książ­ki (Zada­nia sta­ro­pol­skie, „Mate­ma­ty­ka”, nr 4/1957). Źró­dłem był napi­sa­ny przez Józe­fa Tor­żew­skie­go RACHMISTRZ POLSKI.

J. Ziem­ba zacy­to­wał sie­dem­na­ście zadań. Nikt dziś nie będzie na pie­cho­tę szu­kał Radyx Sor­sa­lid, czy­li pier­wiast­ka stop­nia pią­te­go. Ucie­szy­ły mnie jed­nak dwa zada­nia, któ­re przy­da­ły mi się od razu na zaję­ciach ze stu­den­ta­mi peda­go­gi­ki, szy­ku­ją­cy­mi się do pra­cy z naj­młod­szy­mi ucznia­mi szkół pod­sta­wo­wych. Tym razem wspo­mnę o jed­nym zadaniu.

Ieden Pocz­tarż bie­ga co dzień mil 10. dru­gi zaś bie­ga pierw­sze­go dnia milę, dru­gie­go 2. mile, trze­cie­go 3. y tak con­se­qu­en­ter iak Pro­gres­sa Aryt­me­tycz­na. Quaer. ieże­li­by dwa Pocz­tar­że ied­nym dniem wyszli z Mia­sta, kto­re­go dnia by jeden dru­gie­go dognał?

Sądzę, że żad­nych obja­śnień nie potrze­ba – wszyst­kie­go stop­nio­wo moż­na się domy­ślić. Prze­brnię­cie przez to dziw­ne sfor­mu­ło­wa­nie jest tyl­ko małym ćwi­cze­niem czy­ta­nia ze zro­zu­mie­niem… Czy Pocz­tarż to posła­niec? A przy oka­zji – jak wyso­kie mamy teraz wyma­ga­nia co do kon­se­kwent­nej pisow­ni i uni­ka­nia wyra­zów (zbyt) obcych?

Jest wie­le metod roz­wią­za­nia tego zada­nia. Dwa róż­ne spo­so­by są chy­ba natych­miast oczy­wi­ste. Pod­su­wa­łem je oso­bom w róż­nym wie­ku i z róż­nym mate­ma­tycz­nym doświad­cze­niem. Naj­cie­kaw­sze roz­wią­za­nie usły­sza­łem od dwunasto- czy trzynastolatka

Usły­sza­łem, bo nie widzia­łem. Kart­ka leża­ła bez­czyn­nie na sto­le, a mój roz­mów­ca patrzył w sufit. Moja cier­pli­wość była wysta­wio­na na próbę.

Wresz­cie zaczął mówić:
– Dzie­sią­te­go dnia obaj prze­bie­gną tyle samo. A co dzie­wią­te­go dnia jeden stra­cił, to jede­na­ste­go odzy­ska. Co ósme­go… to dwu­na­ste­go… Tak, dzie­sią­ty dzień będzie środ­ko­wy. Dwa­dzie­ścia! Nie… Jest środ­ko­wy, więc nie­pa­rzy­ście. Dziewiętnaście!

To było zna­ko­mi­te wyko­rzy­sta­nie syme­trii. Trze­ba ją tyl­ko naj­pierw zauważyć…

Zakoń­cze­nie
Temat niniej­sze­go cyklu jest nie­zwy­kle boga­ty i moż­na by jesz­cze bar­dzo dużo dodać. Spo­ro mie­li­by do powie­dze­nia muzy­cy, fizy­cy i arty­ści czy archi­tek­ci. Prze­ja­wy syme­trii ota­cza­ją nas wszę­dzie. Zmie­rzam już do koń­ca – trze­ba umieć kie­dyś powie­dzieć: dość.

Zachę­cam Cię, Czy­tel­ni­ku, do uważ­ne­go patrze­nia wszę­dzie: i w ogro­dzie, i na uli­cy, i nad wodą, i w lesie.

Co takie­go jest pod nogami?

Zachę­cam do sta­wia­nia pytań co dalej? czy to pasu­je? czy powtó­rze­nie jest wier­ne? jak to wyglą­da do góry noga­mi? itd..

Rośli­ny zna­ko­mi­cie zna­ją symetrię.

Zasta­na­wia mnie wraż­li­wość geo­me­trycz­na i este­tycz­na pro­jek­tan­ta ulicz­nej meta­lo­wej kla­py, na któ­rą się nie­daw­no natkną­łem pod­czas spa­ce­ru. Na jaką syme­trię zwra­cał naj­więk­szą uwa­gę? O co mu cho­dzi­ło? Ta kla­pa – z zupeł­nie pomie­sza­ny­mi syme­tria­mi obro­to­wy­mi – tra­fi­ła na wizu­al­ny „uskok” chod­ni­ka, gdzie się spo­ty­ka­ją nie­pa­su­ją­ce do sie­bie par­kie­ta­żo­we wzo­ry kost­ki brukowej…

Patrz­my wkoło!

Jan Bara­now­ski